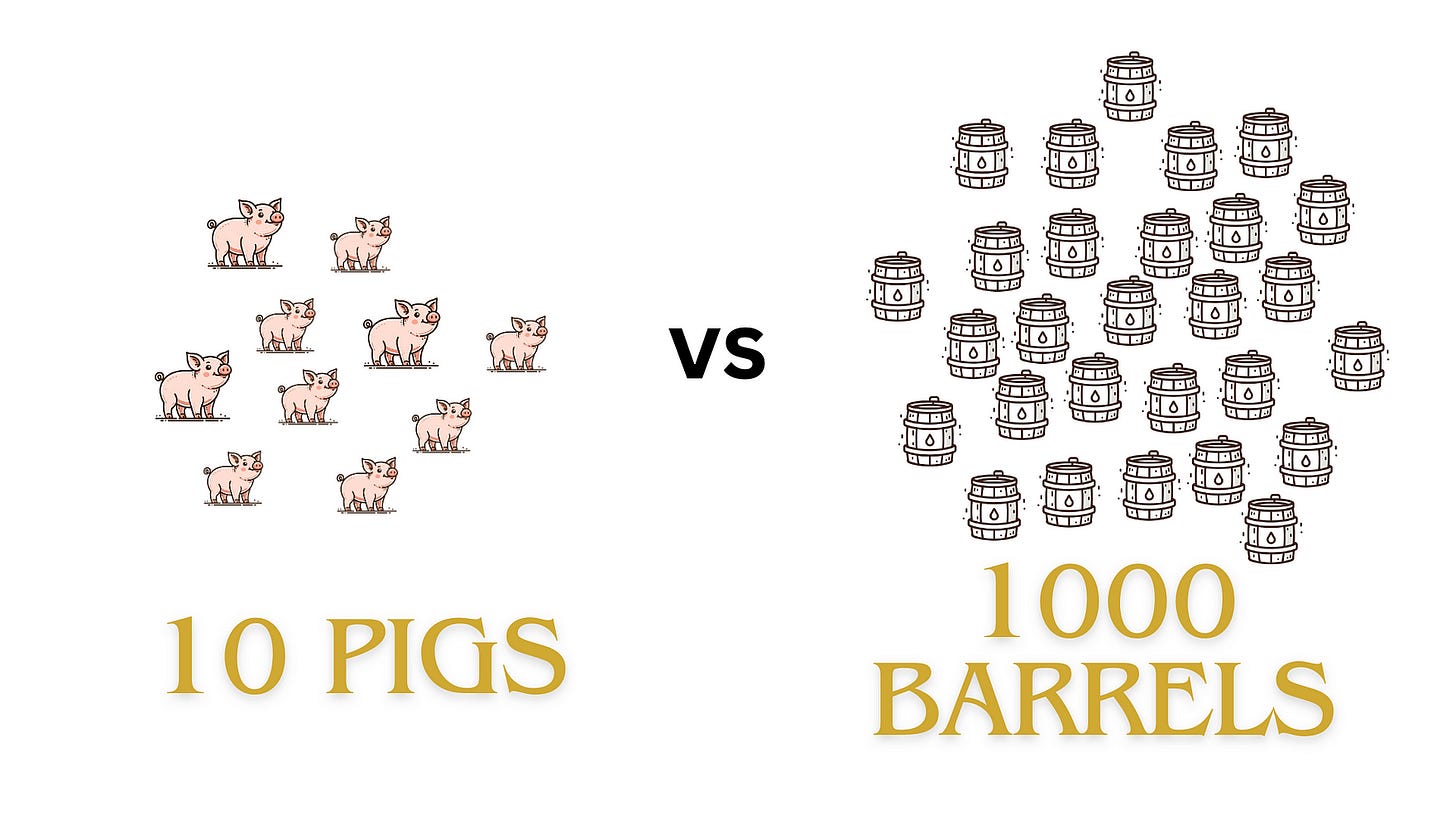
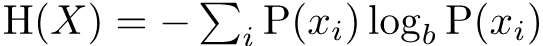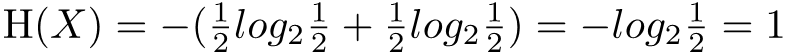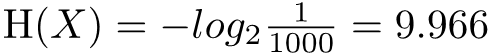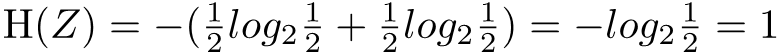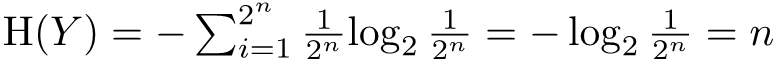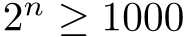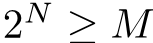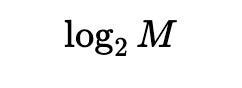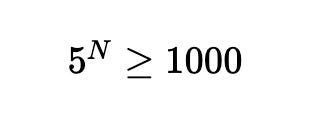Minimum Pigs Required to Find One Poisonous Barrel out of 1000 Within an Hour, Given Pigs Die Within 15 Minutes of Drinking Poison
The best explanation on the Internet.
Here is a classic interview question:
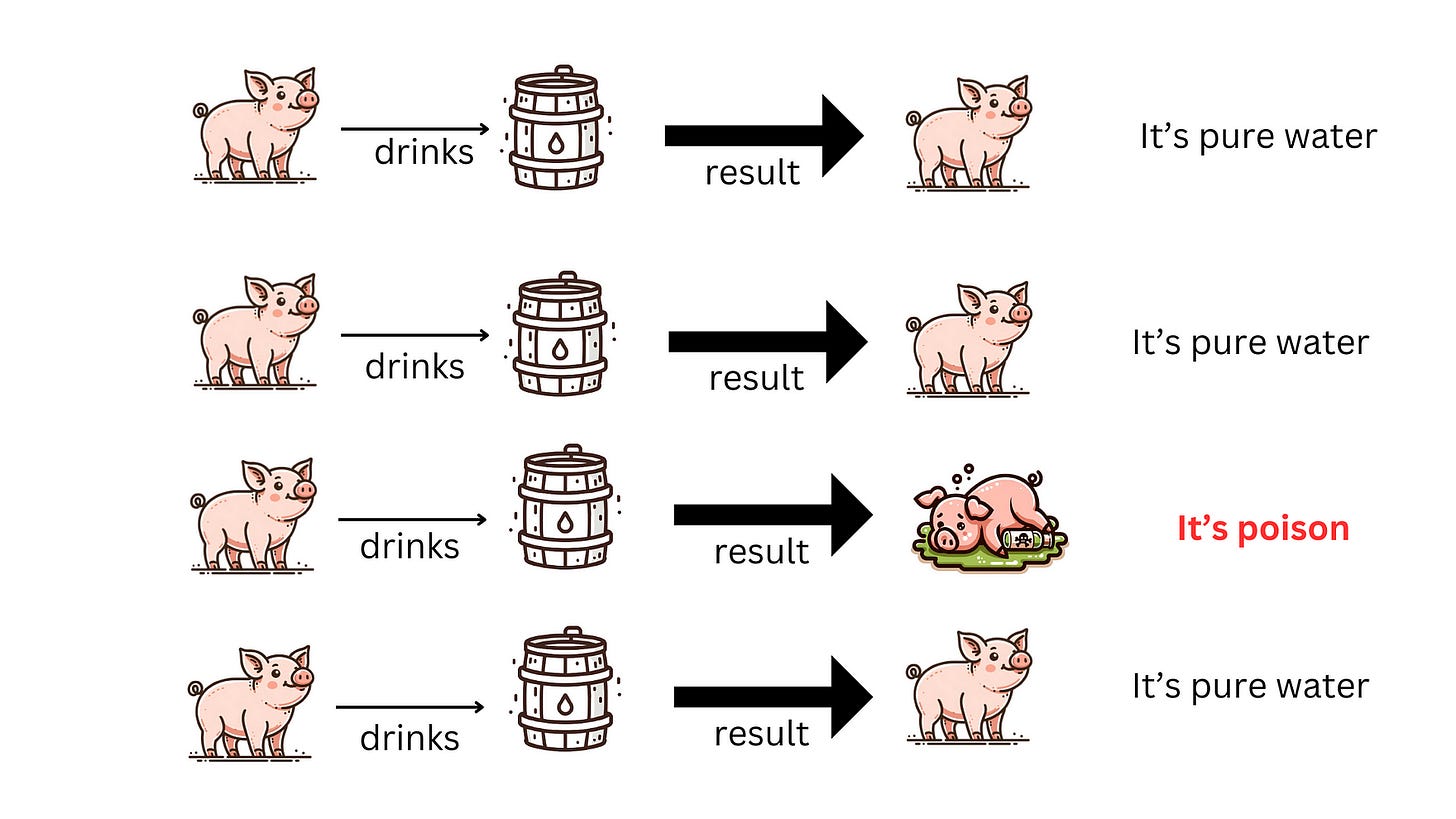
There are 1000 barrels of water.
One (and only one) of them contains poison, the rest of them are pure water.
They all look the same.
A single drop of poisoned water is sufficient to cause the death of a pig.
If a pig drinks that poison, it will die within 15 minutes. Note that death occurs within 15 minutes. It may be 1 minute after drinking the poison, or it may be 10 minutes after drinking the poison.
The death is solely caused by the poisoned water; no other factors will lead to the pig’s demise.
The pig’s capacity to consume water is unlimited, and it is assumed that it takes zero time to drink any water.
What is the minimum number of pigs you need to figure out which barrel contains the poison within 1 hour?
You may have already seen similar articles elsewhere, but I can assure you, this one will be the clearest, most detailed, and most insightful article you’ve come across. If you can find a better article than this one, I will pay you 100 US dollars.
The Dumbest but Intuitive Solution: 1000 Pigs
Before we find out the best solution, we can find an intuitive one.
There are 1000 barrels, so we can literally use 1000 pigs for the test. Each pig drinks a barrel of water. If a pig dies, the corresponding barrel contains poison.
In this solution, we need 1000 pigs.
We have 60 minutes: 250 Pigs
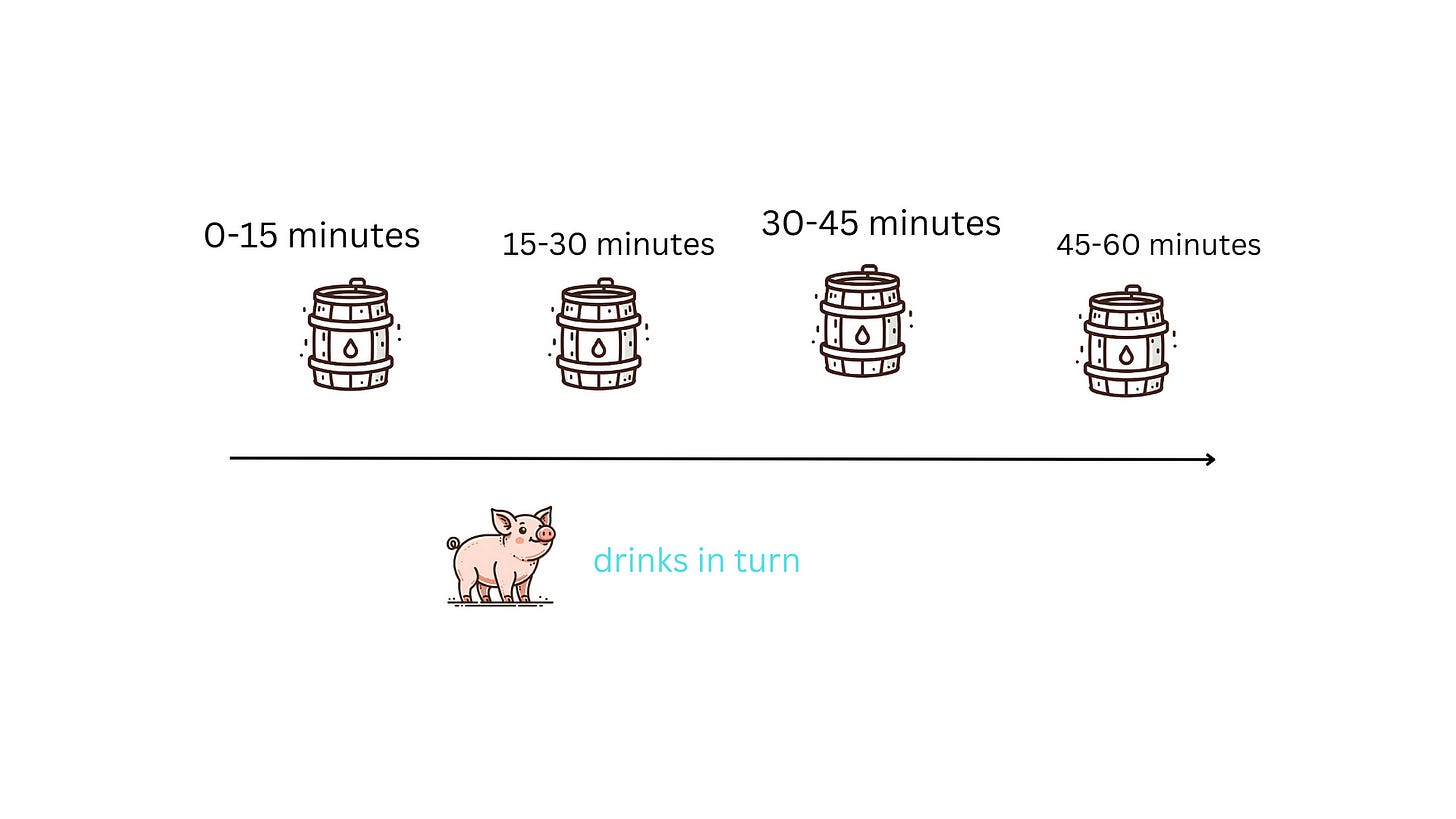
In 1 hour, one pig can be used 4 times:
Drink the first barrel of water at the 0th minute.
If it’s not dead, drink the second barrel of water at 15th minute.
If it's not dead, drink the third barrel of water at 30th minute.
If it’s still not dead, drink the 4th barrel of water at 45th minute.
One pig responds with four barrels, we can test 1000 barrels of water in 1 hour with 250 pigs.
Even though we optimized the solution, 250 pigs are still too many. Is there a better solution?
We can mix the water: 100 Pigs
Of course, we can.
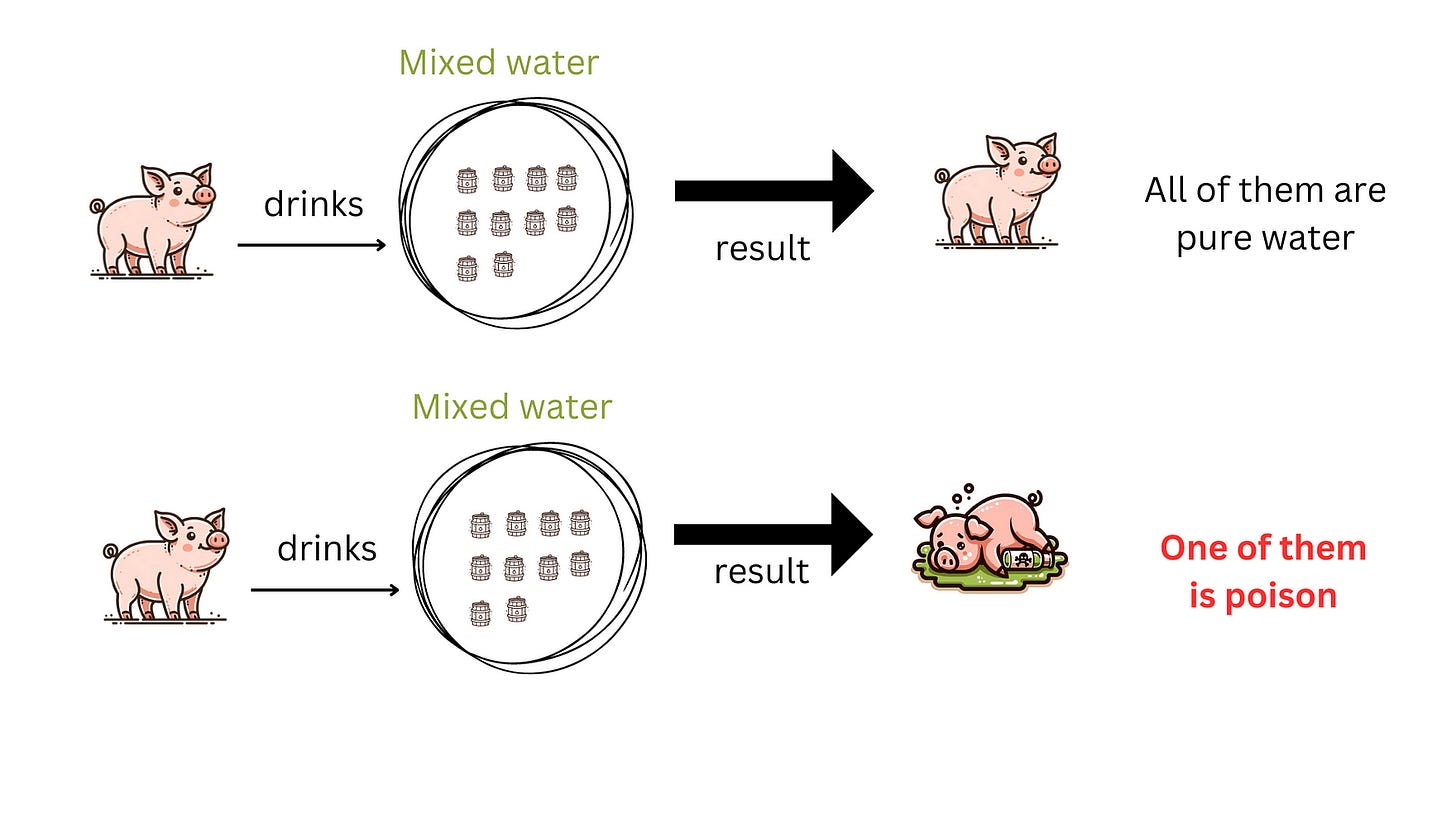
In the above solutions, one pig was used to test only one barrel for each 15-minute. But, we can mix the water!
We can take a portion of water from each of several barrels, mix them together, and feed it to a pig. If the pig does not die within 15 minutes, it indicates that none of these barrels of water contain poison. If the pig dies, it means the poison is in one of these barrels. Although we still don’t know in which specific barrel the poison is, we can continue to test these barrels of water until we find the poison.
Assuming we now have 100 pigs:
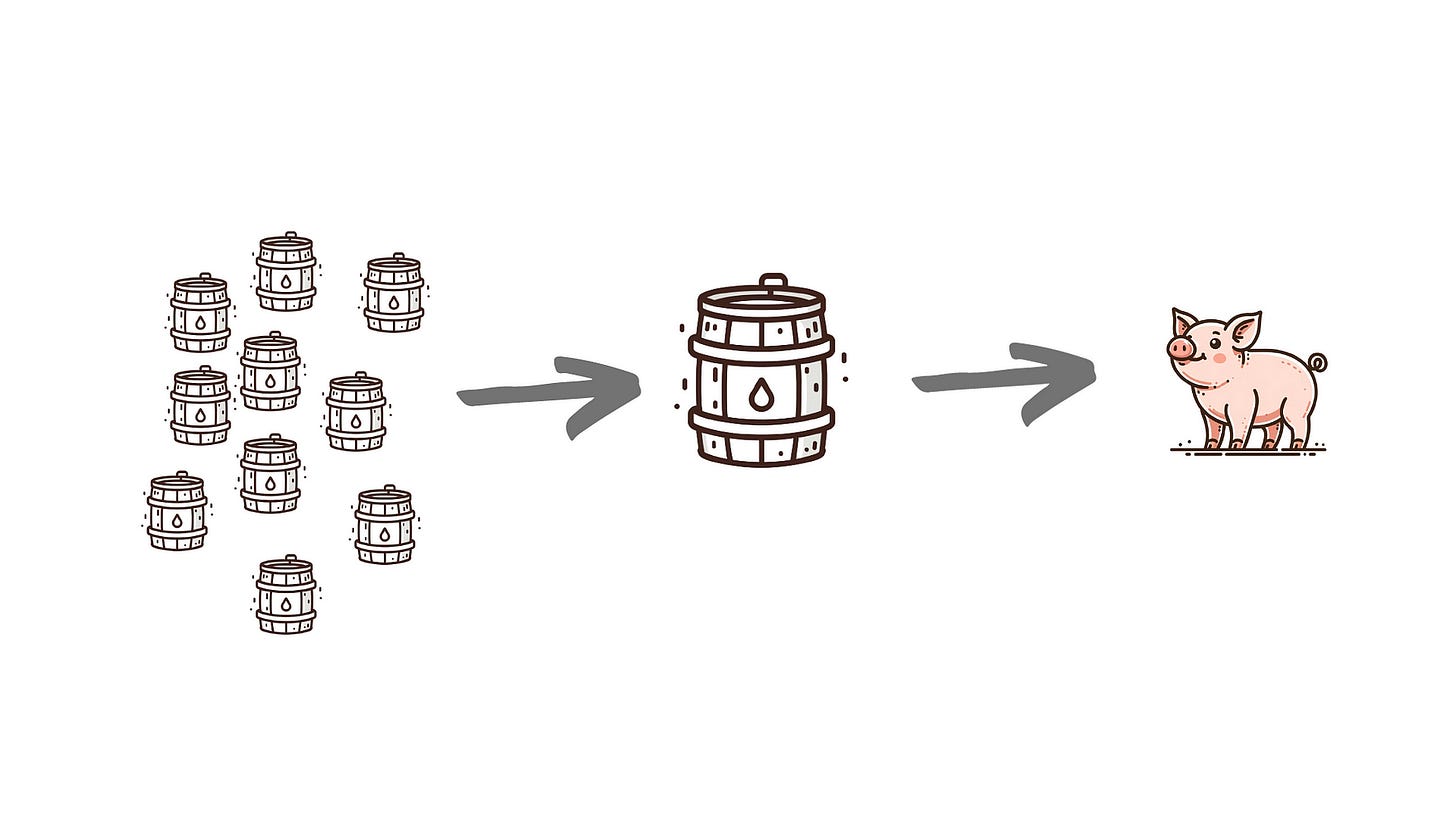
In the first round, we can mix every 10 barrels of water into one, thus accumulating 100 barrels of mixed water.
Then we feed each mixed bucket to one of the 100 pigs. After 15 minutes, one of the pigs will die, and from this, we will know which set of 10 barrels contains the poison.
In the second round, we feed these 10 individual barrels to 10 different pigs, and after another 15 minutes, we will know the answer.
In this solution, we’ve made a significant breakthrough in our thinking: each pig can test multiple barrels of water at the same time! Then, by conducting several rounds of testing, we can identify the barrel that is poisonous.
Reduce pigs: 10 Pigs
The previous plan was effective; we found the poison with just 100 pigs. However, we’ve realized that 100 pigs are clearly more than necessary; it seems we don’t need that many.
So, how many pigs would be appropriate? Would 10 be sufficient? Let’s do the math.
In the first round, we can mix every 100 barrels of water into one, thus accumulating 10 barrels of mixed water.
Then we feed each mixed barrel to one of the 10 pigs. After 15 minutes, one of the pigs will die, and from this, we will know which set of 100 barrels contains the poison.
Now, we know that the poison is hidden among these 100 barrels of water, and we still have 9 pigs left.
In the second round, we can divide the 100 barrels of water into 9 parts, with 8 parts consisting of mixtures from 11 barrels each, and one part being a mixture from 12 barrels.
Then we feed each mixed barrel to one of the 9 pigs. After 15 minutes, one of the pigs will die, and from this, we will know which set of barrels contains the poison.
Suppose the poisoned water is among those 12 barrels.
Now we used 30 minutes, and 8 pigs left for 12 barrels.
Obviously, we can find the poisonous one easily.
From the results above, it seems that 10 pigs are still too many; there should be a better plan that uses even fewer pigs. But how many exactly? 9, 8, 5, or perhaps 4? Do we have to try one by one? Is there any ultimate solution?
Alright, thank you very much for reading this far. But I am sorry to say, the solution above is completely incorrect.
Indeed, we can optimize our plan through some trials, but aimless thinking will not lead us to the best solution.
For elementary and middle school students, these methods might suffice, but if you aspire to join a major tech company, you need to upgrade your way of thinking.
The reason I listed the solutions above is that: that’s how I used to think as well.
In the beginning, it’s okay to have some incorrect approaches, as long as we are willing to learn.
In many articles, some authors will directly tell you the correct answer, but they don’t explain why it is the answer. Here, we not only need to learn how to solve this problem, but we also need to learn how to solve similar types of problems. That way, everyone can draw analogies from one another, apply the knowledge broadly, and solve all similar problems.
Dude, let’s start our adventure to this great thinking!
2 Pig, 2 Barrels
The original problem is a little bit complex, let’s simplify it to a simple one:
With 2 pigs and 2 barrels of water, one of which is poisoned, how do you find out which barrel contains the poison within 15 minutes?
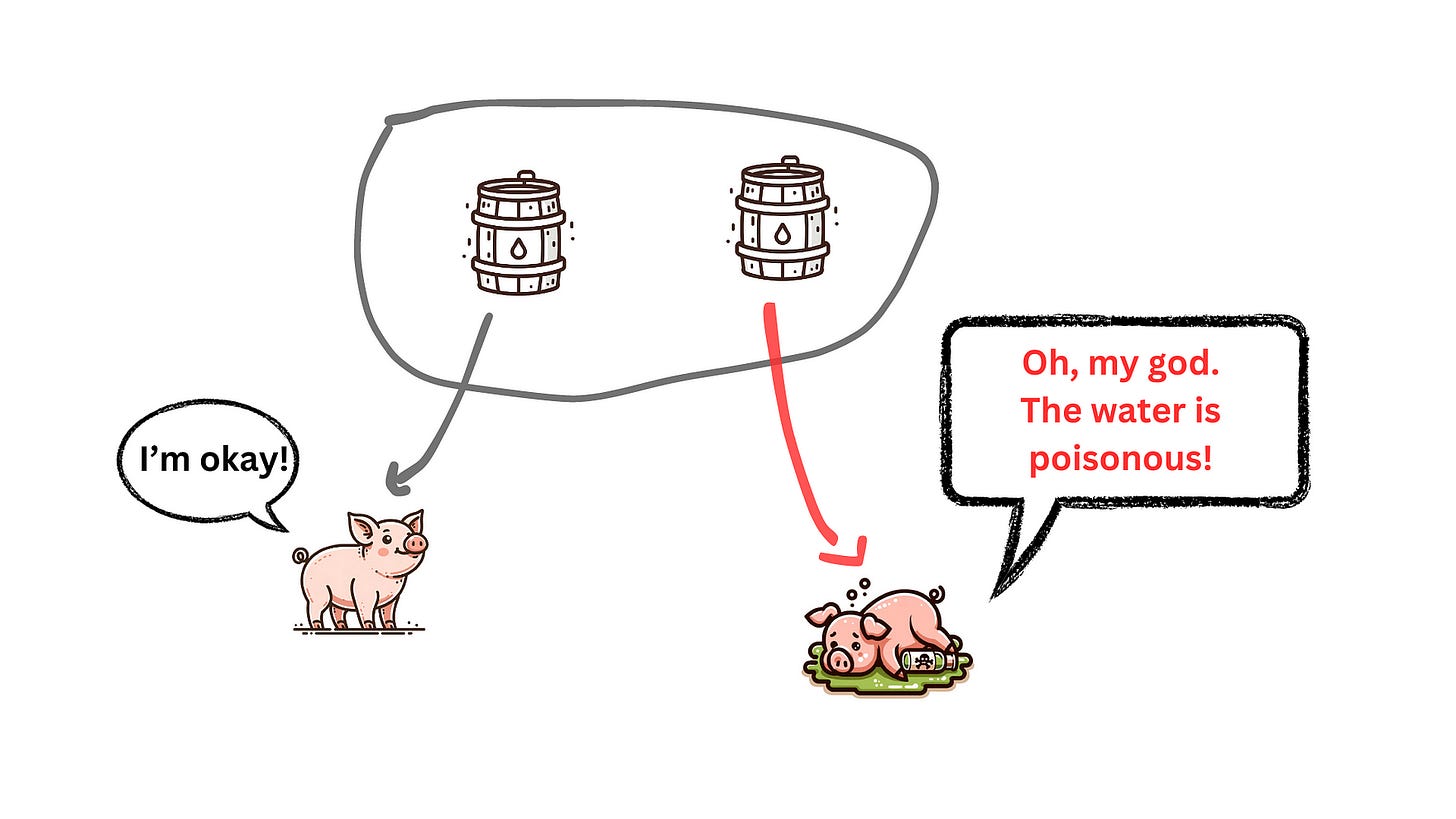
This is simple: have each pig drink from one barrel of water. The pig that dies will indicate which barrel contains the poison.
2 Pigs, 3 Barrels
Now upgrade the problem:
With 2 pigs and 3 barrels of water, one of which is poisoned, how do you find out which barrel contains the poison within 15 minutes?
The principle is the same: have each pig drink from one barrel of water. The pig that dies will indicate which barrel contains the poison. If neither pig dies, then it means the third barrel of water is poisoned.
2 Pigs, 4 Barrels
Now upgrade the problem:
With 2 pigs and 4 barrels of water, one of which is poisoned, how do you find out which barrel contains the poison within 15 minutes?
This time, some tricks are required.
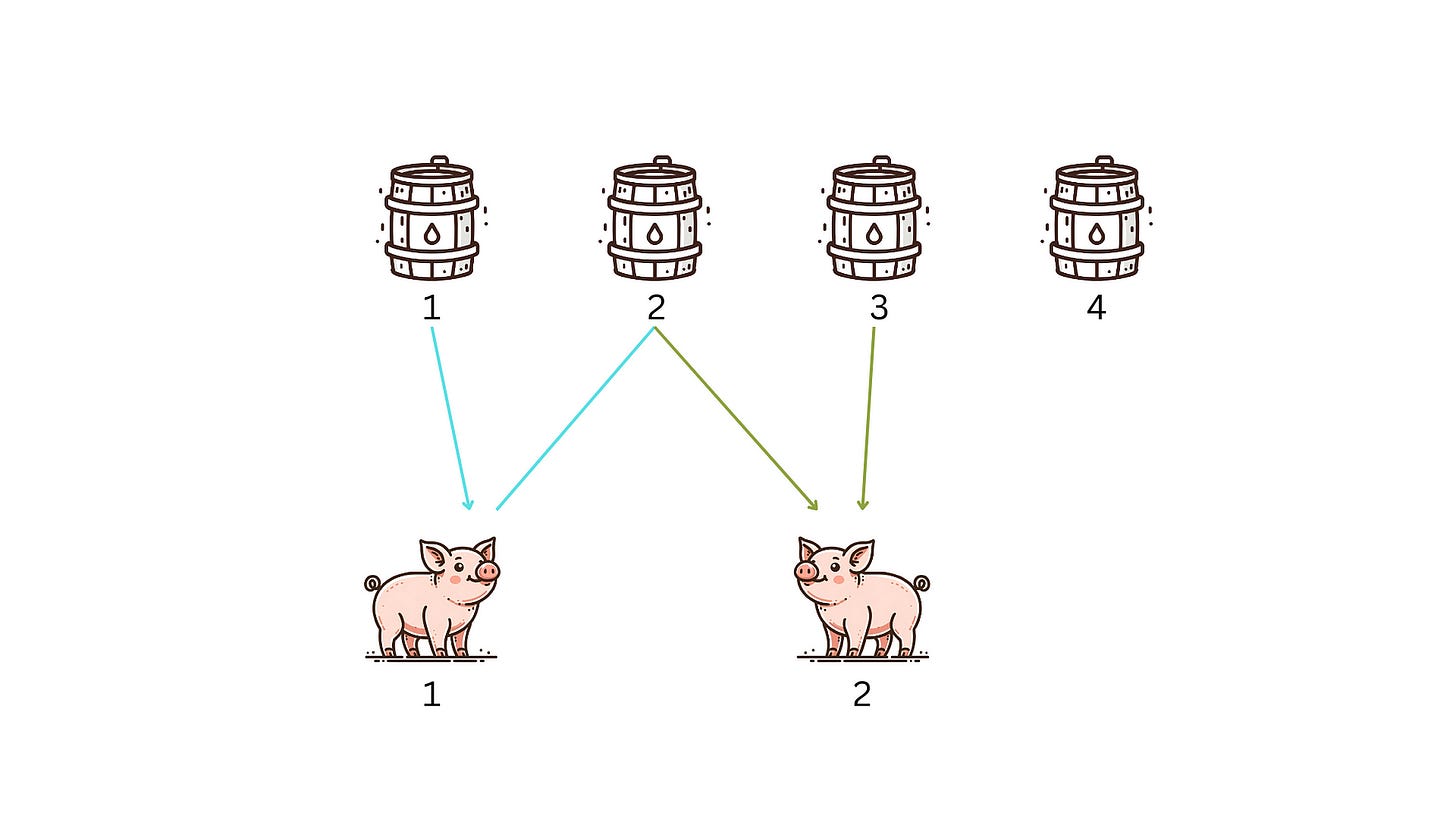
For ease of description, let’s assume the barrels of water are numbered 1, 2, 3, and 4, and the pigs are numbered 1, and 2.
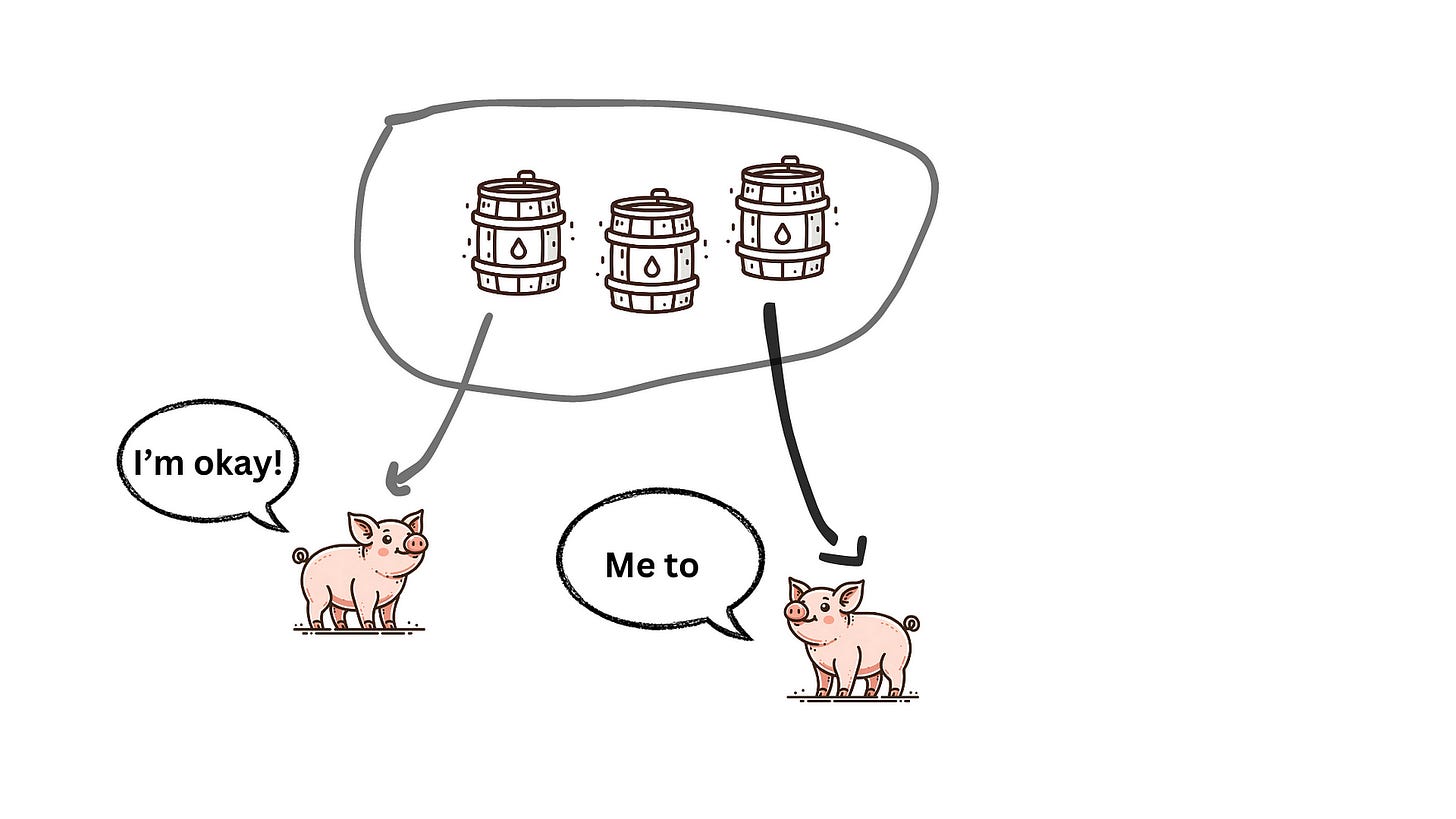
Pig1 drinks from barrel1 and barrel2, while Pig2 drinks from barrel2 and barrel3.
If Pig 1 and Pig 2 survive, it indicates that barrels 1, 2, and 3 are not poisoned, leading to the conclusion that barrel 4 is poisoned.
If Pig 1 survives and Pig 2 dies, it means barrels 1 and 2 are not poisoned, and one of barrels 2 and 3 is poisoned, leading to the conclusion that barrel 3 is poisoned.
If Pig 1 dies and Pig 2 survives, it indicates that barrel 1 is poisoned.
If Pig 1 dies and Pig 2 also dies, it indicates that barrel 2 is poisoned.
This is a simple deduction, similar to the principles used when playing the game Minesweeper.
In this kind of deduction, we consider the status of both pigs simultaneously, and based on their conditions, we infer the toxicity of the water.
Then, if there are only 2 pigs, can you find the poison in 5 barrels of water?
You can try it yourself.
The correct answer is: that it is impossible to find out within 15 minutes. As for the principle, I will explain it later.
3 Pigs
Now upgrade the problem again:
If we have 3 pigs now, how many barrels of water can we process at most in 15 minutes?
You can try it yourself. I will give the answer directly below.

The answer is 8 barrels of water.
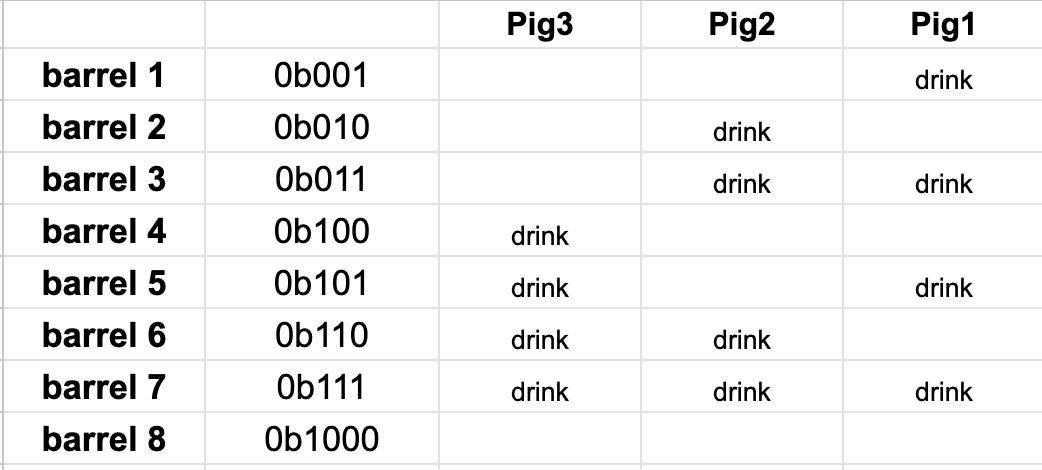
We can create a two-dimensional grid of pigs and barrels. The table has three columns, representing three pigs, and eight rows, representing eight barrels. If the word “drink” is filled in a cell of the grid, it means the piglet should drink the water from that barrel. If it is left blank, it means the piglet does not need to drink from that barrel.
In this way, we can deduce which barrel is poisoned based on the survival status of the piglets.
If all three piglets die, by looking at the chart we can see that they all drank from the seventh barrel, indicating that the water in the seventh barrel is poisoned.
If none of the piglets die, it would indicate that the eighth barrel contains the poison.
If piglets 1 and 2 die, but piglet 3 does not, then it indicates that the third barrel is poisoned.
I understand you may have many questions at this point. Don’t worry, I will answer them one by one.
Why can this plan work? What’s the principle behind it?
The answer is: In order to maximize the use of each piglet, we have each one drink from half of the barrels.
This way, if a piglet dies, it indicates that the poisoned water is among that half; the same logic applies if it survives. In other words, one piglet can eliminate half of the incorrect options.
By applying this method to each piglet, we have three opportunities to halve the pool of potential answers. And since eight divided by 2 three times is one, we arrive at 1, the unique answer.
How do we arrange barrels for each piglet?
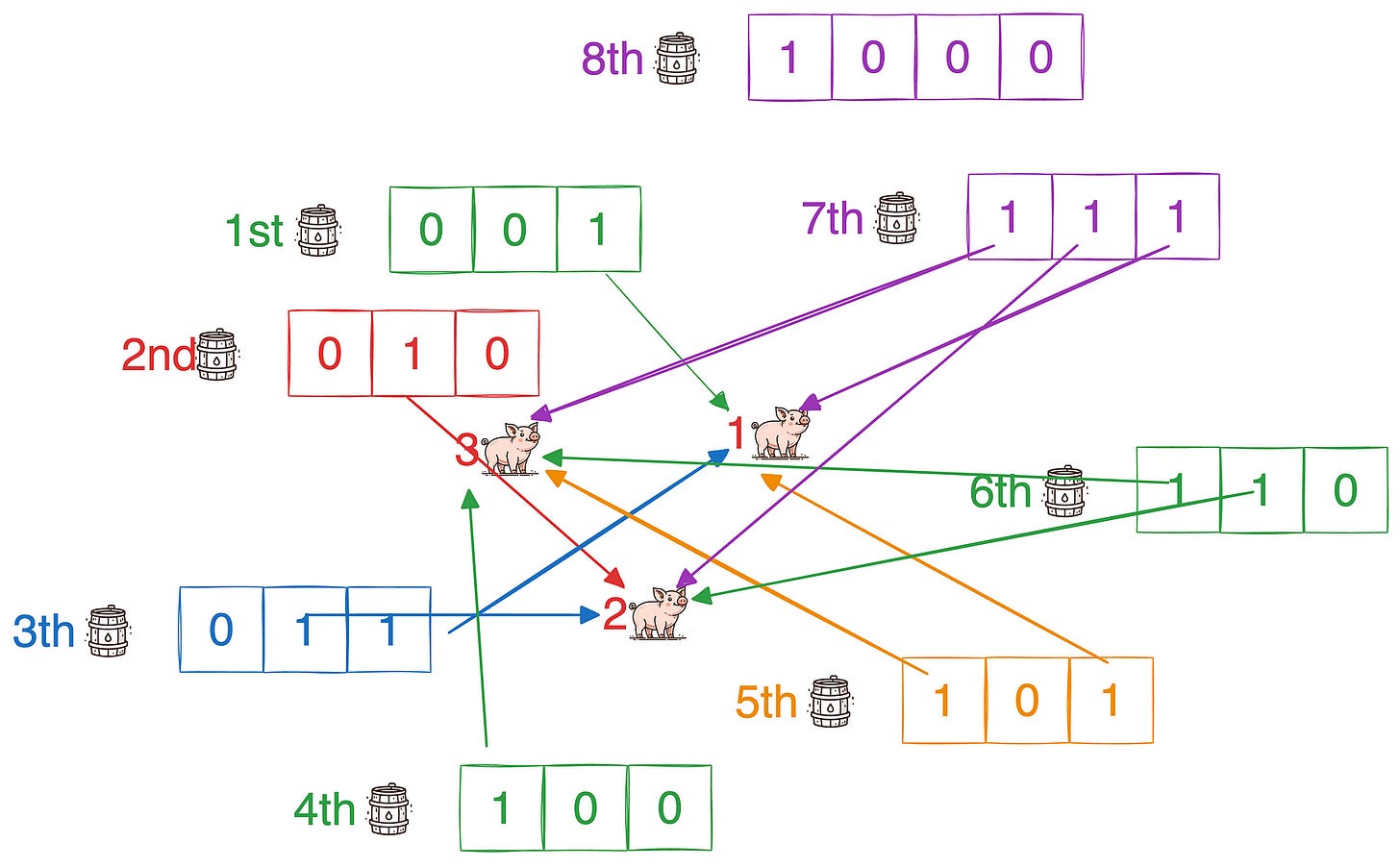
Here we can make use of the characteristics of binary. We first convert the barrel numbers into binary, for example, barrel number 6 corresponds to 0b110.
The first digit from the right is 0, so the first piggy doesn’t drink it.
Its second digit from the right is 1, so the second piggy drinks it.
Its third digit from the right is 1, so the third piggy drinks it.
We can allocate each barrel of water to the appropriate piglet in this manner. Each piglet will drink exactly 4 times.
N pigs, M barrels
Now let’s continue to expand our knowledge:
With N pigs, what’s the maximum number of barrels we can handle?
And with M barrels, what’s the minimum number of pigs we need?
To solve this problem, we need some more complex tools. The following content will be quite in-depth. But my friend, I hope you won’t be afraid.
Remember: the more difficult a concept is, the more competitive you become once you master it. If a concept is simple and everyone knows it, then there’s not much competitive edge in learning it, right?
We know that doctors belong to the healthcare industry and security guards belong to the security services industry. Do you remember which industry programmers belong to?
The answer is the information technology industry. Here, we begin to discuss some knowledge of information theory.
Information Theory
This problem appears to be about algorithms, but at its core, it’s a question of information theory. Finding the answer to this problem is easy, but learning to think in terms of information theory is quite challenging.
Only when you’ve learned to use information theory to think through problems, you can solve all similar types of issues.
Let’s first supplement some knowledge about information theory.
Entropy in thermodynamics
The concept of entropy originated in physics as a measure of the degree of disorder in a thermodynamic system, that is, the level of chaos in the system.
The law of increasing entropy states:
In an isolated system where no external work is done, the total disorder (entropy) will continuously increase.
The law of increasing entropy informs us that if you mix a cup of hot water with a cup of cold water, without doing any work on the water in the cup, the molecules of hot and cold water will ultimately distribute in the most disordered manner. This means the overall temperature will eventually even out, and there will never be a situation where hot and cold water layers separate.
If we consider the universe as an isolated system, then it must be evolving from an ordered state to a disordered, chaotic one. When the entropy of the universe reaches its maximum value, all other forms of usable energy will have been converted into thermal energy, and all matter will have reached thermal equilibrium. This state is known as the heat death of the universe. In such a universe, no energy remains to sustain movement or life.
Entropy in Information Theory
In information theory, the concept of entropy is analogous to that in thermodynamics and describes the “degree of uncertainty in information.”
Thermodynamic entropy: the degree of chaos in a system
Information entropy: a measure of the uncertainty in information
Thus, the uncertainty in information is akin to the degree of chaos in a thermodynamic system.
This means that the greater the uncertainty in the information, the greater the information entropy. So what kind of information has a high degree of uncertainty?
For example, flipping a coin. If I were to guess heads or tails, I would essentially have to guess blindly because there is a high degree of uncertainty, with both outcomes having a probability of 0.5.
For events like guessing the outcome of a single coin flip, there is a high degree of uncertainty, and thus, the information entropy is also high.
I am almost certain that the sun will rise from the east tomorrow; this is an event with very high certainty, so the information entropy is very low. If the sun really rises from the east tomorrow, then the value of this information content is also very low because it has hardly reduced the uncertainty of the information.
Here are three core concepts: Information, Information Entropy, and Information Content.
They are fundamental concepts in Information Theory, which is a mathematical framework for quantifying information transfer in communication systems.
Information
In the context of Information Theory, information is not about the content or meaning but rather the reduction of uncertainty. When we receive a message, information is the part that tells us something we did not know before, which reduces uncertainty about some state of the world or a given situation.
Information Entropy
Information entropy, often just called entropy in this context, is a measure of the uncertainty or unpredictability of a system’s state. It quantifies the average amount of information produced by a stochastic source of data. For a given probability distribution over events, the entropy is maximized when all events are equally likely, and it is zero when the occurrence of one of the events is certain. Entropy is usually denoted by the letter H and is measured in bits (if the logarithm is base 2), which corresponds to the amount of information required to encode the outcome.
Information Content
Information content, also known as self-information, is the amount of information associated with the occurrence of a particular event. It is inversely related to the probability of the event: the less probable an event is, the more information its occurrence conveys.
Each of these concepts plays a crucial role in various fields such as data compression, cryptography, and communications, among others.
Shannon defined the entropy Η of a random variable X as follows, with the value range being {x1, …, xn}.
\mathrm{H} (X)=-\sum _{{i}}{{\mathrm {P}}(x_{i})\log _{b}{\mathrm {P}}(x_{i})}b is the base used for logarithms. When b = 2, the unit of entropy is bit.
P is the probability mass function of X, which we can understand as the probability of event xi occurring.
The formula looks scary, but it’s actually very simple.
Let’s use the example of flipping a coin. The information entropy of random variable Flipping a coin and it landing heads up is:
\mathrm{H} (X)=-(\frac{1}{2}log _{2}\frac{1}{2} + \frac{1}{2}log _{2}\frac{1}{2}) = -log_{2}\frac{1}{2}=1That is to say, the information entropy of the event that a coin toss is heads only requires 1 bit, that is, only a 1-bit binary number can be used to represent the size of this information.
Back to the Problem
Even if you don’t understand the above formula, it doesn’t matter. I will calculate it with you!
With such a theoretical weapon, we can do some precise calculations.
With 1000 barrels, in 15 minutes, what’s the minimum number of pigs we need?
The information entropy of the random variable (one of 1,000 barrels of water is poisonous) is:
\mathrm{H} (X)=-log _{2}\frac{1}{1000} =9.966A pig will either live or die after drinking water. There are two states in total. Therefore the information entropy of (the state of a pig after drinking water) Z is:
\mathrm{H} (Z)=-(\frac{1}{2}log _{2}\frac{1}{2} + \frac{1}{2}log _{2}\frac{1}{2}) = -log_{2}\frac{1}{2}=1Here you may ask: The probabilities of pig survival and death are not equal. Why do you use the probability of 1/2 to calculate?
This is because when calculating information entropy, we consider the maximum information entropy that can be expressed by n pigs.
Mathematically it can be proved that when random events occur with equal probability, information entropy is maximum.
The question requires at least n pigs, which means that in the worst case, poisonous water can be found with n pigs. The worst case scenario is that the probability of life and death for each pig is equal.
Therefore, we use the equal probability method to find the smallest n at the maximum information entropy. When n is smaller, 1000 barrels of water cannot be measured in the worst case.
n pigs will have 2^n states after drinking water, the information entropy of (the state of n pigs after drinking water) Y is:
\mathrm{H} (Y)=-\sum _{{i=1}}^{2^n}{\frac{1}{2^n}}{\log _{2}{\frac{1}{2^n}}}=-\log _{2}{\frac{1}{2^n}}=nTherefore, according to the question requirements, if at least n pigs are needed to find the barrel of poisonous water, then the information entropy of the random variable Y must be greater than the information entropy of the random variable X, that is
H(Y) >= H(X)
that is, n >= 9.966, or n = 10.
After we use information entropy to calculate the minimum value of n, we can firmly believe that n=10 must be the optimal solution in theory. Any attempt to find a value less than 10 is in vain.
In fact, the simplified version of the above information entropy calculation can be written in the following more understandable form:
Alright, you can forget all the previous formulas; just remember this one — it can solve all the problems.
With N pigs, the maximum number of barrels we can handle is 2 ^ N
And with M barrels, what’s the minimum number of pigs we need is an integer that greater than
If there are 3 pigs, the maximum number of barrels we can handle is
2 ^ 3 = 8If there are 4 pigs, the maximum number of barrels we can handle is
2 ^ 4 = 16If there are 10 pigs, the maximum number of barrels we can handle is
2 ^ 10 = 1024With 100 barrels, what’s the minimum number of pigs we need is 7
With 300 barrels, what’s the minimum number of pigs we need is 8
With 3000 barrels, what’s the minimum number of pigs we need is 11
Do you see that? This is the power of information theory. Now, if you’re in an interview and the interviewer poses a similar question, you can find the most correct answer within 10 seconds!
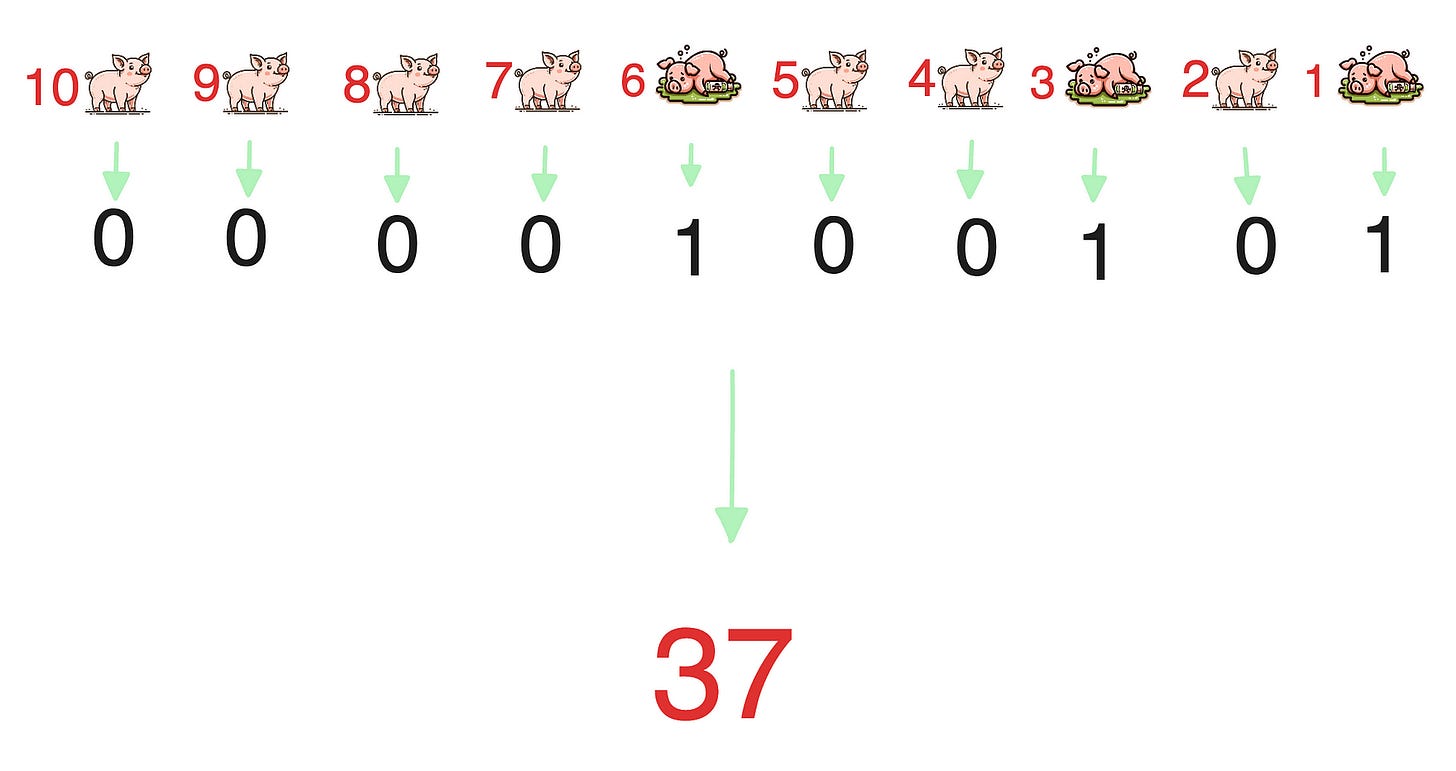
So how should these 1,000 barrels of water be distributed? Similar to our previous three-pigs problem, we can convert the barrel numbers to binary and then allocate the water to the designated piglets.
If after the test, pigs number 1, 3, and 6 die while the others survive, then it indicates that the poisonous barrel’s number is
0b0000100101, that is 37.
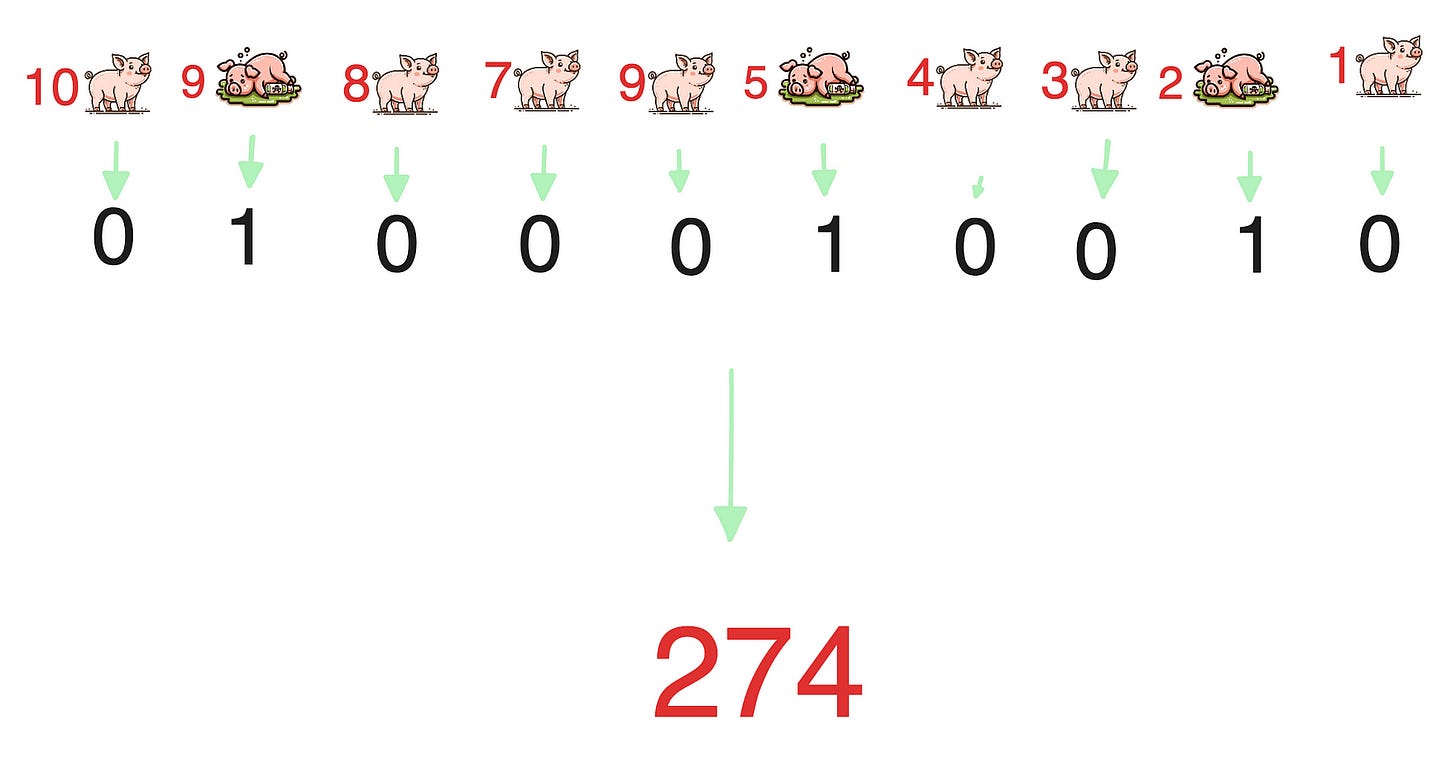
If after the test, pigs number 2, 5, and 9 die while the others survive, then it indicates that the poisonous barrel’s number is
0b0100010010, that is 274.
God Like
The knowledge points above can solve the vast majority of problems. However, the problem posed in our title is a bit more difficult because it involves rounds. Given one hour, and with each round taking 15 minutes to complete, how should we plan for this problem?
With 1000 barrels, in 60 minutes, what’s the minimum number of pigs we need?
If you can understand this issue, then in this type of problem, no interview will be a challenge for you.
In the previous problem, there were only 15 minutes, which means each pig could only drink water in one round. After the test, the pigs have only two states: alive or dead.
Now, with 60 minutes available, four rounds of testing can be conducted. To fully utilize each pig, we should obviously try to have each one drink in all four rounds.
Therefore, after one hour, a pig could have five possible states:
Dies within 0–15 minutes
Dies within 15–30 minutes
Dies within 30–45 minutes
Dies within 45–60 minutes
Still alive after one hour
This means that one pig can convey information equivalent to 5. We just need to ensure:
The minimum value of N is 5. So we need 5 pigs.
How about it? After learning information theory, we can solve such problems in seconds?
However, even though we know that we only need five pigs to identify the poisonous barrel out of 1,000 in one hour, how exactly should we go about doing it?
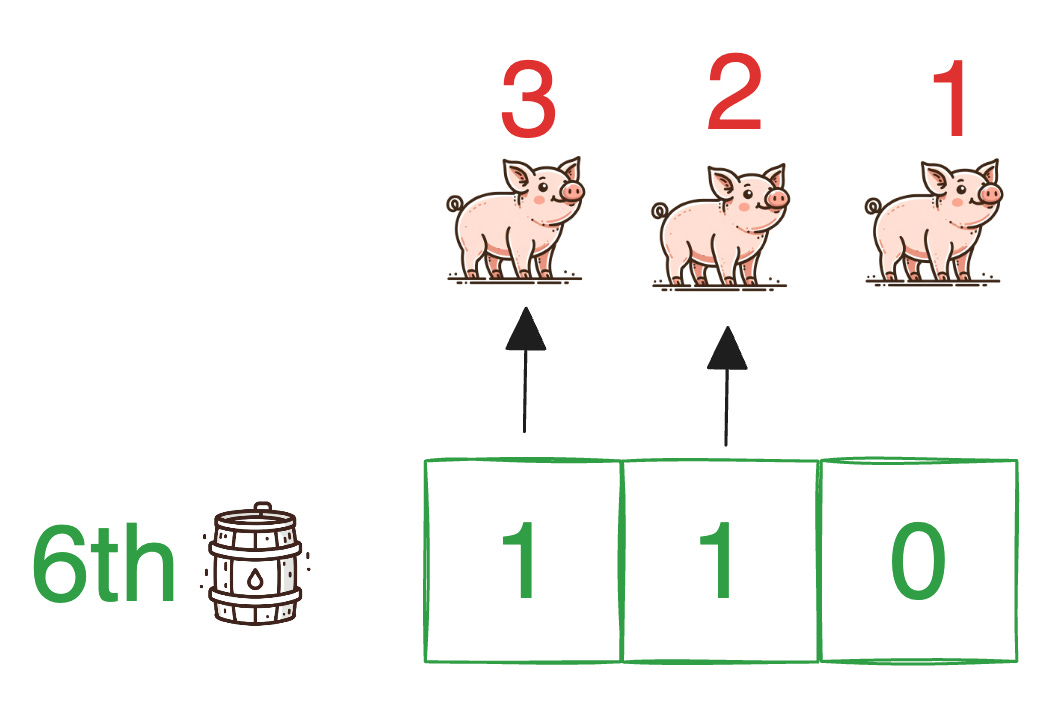
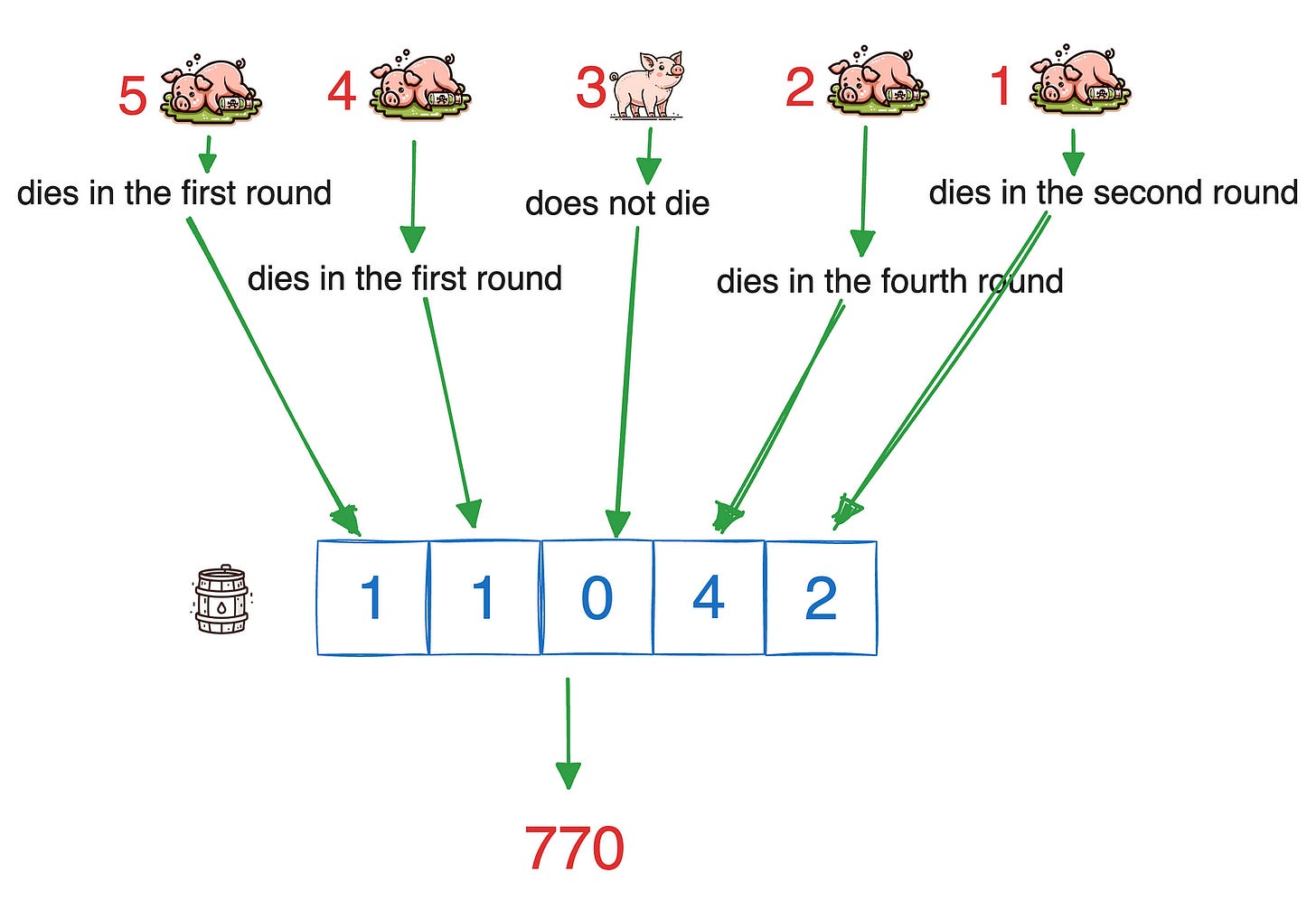
The principle is the same as before, but this time we need to use a base-5 system because a pig can be in one of five states.
If after one hour, Pig 1 dies in the second round, Pig 2 dies in the fourth round, Pig 3 does not die, Pig 4 dies in the first round, and Pig 5 dies in the first round, then the poisonous barrel would be the barrel quinary11042 , that is 772.
Moreover, we know that 5 to the power of 5 equals 3125, so five pigs are more than capable of dealing with 3125 barrels of water. Having them handle 1000 barrels is well within their capacity!
Practice
Just as I promised earlier, after learning from this article, you can immediately calculate the answers to all problems of the same type. Here, let’s look at some examples.
1. Reddit & StackExchange
Here is a question posted on Reddit and StackExchange:
There 1,000 buckets, one of them contains poison, the rest of them are filled with water. They all look the same. If a pig drinks that poison, it will die within 30 minutes. What is the minimum number of pigs to you need to figure out which bucket contains the poison within one hour?
This problem is almost identical to ours, with the only difference being that the poison takes 30 minutes to take effect. Do you know how to calculate it?
Since the poison takes 30 minutes to take effect and we only have one hour, that means we have two rounds. After two rounds, a pig can be in one of three states: dead after the first round, dead after the second round, or not dead at all.
Therefore, we need to ensure:
3 ^ N ≥ 1000
That is:
We need 7 pigs!
2. Poor Rats
Another classic interview question is:
You have 1000 wine bottles, one of which is poisoned. You want to determine which bottle is poisoned by feeding the wine to the rats. The poisoned wine takes one hour to work. How many rats are necessary to find the poisoned bottle in one hour?
After studying the previous articles, this question should be very simple for you. Now the poor piggy has been replaced by a poor mouse. This time the poison takes 1 hour to work, so we only have one chance to experiment.
After an hour, the mouse may be in two states: alive or dead. So the base here should be 2.
2 ^ N ≥ 1000
So we need 10 rats.
Thanks for Reading. Good Nights!